Маятник Ньютона з Багаторазовими Ударними Навантаженнями: Моделювання та Експеримент

1.06.2016

Маятник Ньютона з Багаторазовими Ударними Навантаженнями: Моделювання та Експеримент

Original: http://robotics.cs.iastate.edu/ResearchNewtonsCradle.shtml

У цій темі ми моделюємо зіткнення з декількома тіла в імпульсному просторі у вигляді діаграми стану переходу. Кожне стан описує різну топологію зіткнення характеризується безліччю миттєво активних контактів. У стані, (нормальні) імпульси пов’язані диференційовано з урахуванням відносних жорсткостей в активних точках контакту і енергії деформації, що зберігаються там. Такий зв’язок може привести до перезапуску стиснення від реституції протягом одного удару. Імпульси ростуть уздовж обмеженої кривою з безперервності першого порядку, і сходяться під час переходів між станами.

Впроваджена діаграма станів розпадається зіткнення з декількома тіло в стан послідовності, кожна з яких представляє окрему підгрупу контактів, які миттєво активні під час зіткнення. Там може бути до 2 ^ N станів, багато з яких не можуть з’явитися при зіткненні. Ми створюємо діаграму переходу на льоту, починаючи з початкового стану, коли всі контакти активні. Перехід призводить або новий стан (згенерованого) або до вже сформованого держави. Перехід від одного стану до іншого відбувається, коли небудь вплив закінчує реституцію або неактивний контакт активується, тому що два Зацікавленість об’єкти знову наближаються одна до одної. Кожен контакт пов’язаний з енергійним коефіцієнтом відновлення, що задає повернення фіксованої частини енергії деформації, що зберігається в контакті під час стиснення. Вплив на цей контакт пов’язаний з, що на іншому контакті диференційовано, як визначено за їх відносної жорсткості і співвідношення між їх збережених енергій деформації. Оскільки кожне вплив може залежати від іншого впливу, він може пройти через кілька етапів стиснення і відновлення. Діаграма переходу припиняється, як тільки кінцевий стан без будь-яких активних контактів досягається.

Моделювання маятника Ньютона

Проблема колиски Ньютона добре відомо для декількох впливів. Система була вивчена в якості орієнтира для багаторазових впливів. люлька Типовий Ньютона складається з ряду однакового розміру куль, підвішених в металевій рамі таким чином, що вони просто стикаються один з одним в стані спокою. Кожен шар прикріплений до рами за допомогою двох проводів однакової довжини спрямована під кутом один до одного. Це обмежує руху маятників “однієї і тієї ж площині.

При відсутності замкнутої формі рішення звичайних диференціальних рівнянь для похідних енергії по імпульсу, і імпульсу по відношенню до первинного impluse, еволюція стану моделюється за допомогою за допомогою чисельного інтегрування. На кожному кроці інтегрування, ми перевіряємо, чи був тільки що закінчилося стиснення або впливу, і якщо це так масштабувати відповідну енергію деформації відповідним чином, щоб визнати втрати енергії. І держава транзити, коли енергія деформації деякого кулі в контактній наборі зменшується до нуля під час відновлення. Ініціалізація інтеграції досягається наступним чином. В Енергії Вихідна апроксимувати похідних імпульсу, а потім на основі диференціальних відносин, які вони в кінцевому підсумку описується квадратичною системою, яка вирішується за допомогою методу гомотопічний продовження.

При моделюванні, ланцюг за участю п’яти куль, встановлених як зазначено вище, буде проводити розслідування на основі моделі багаторазового впливу ми ввели. Всі кулі в ланцюзі є ідентичним. Контакти між кулями розглядаються як точкові контакти і змодельовані як Hertz контакт, в якому сила представляється у вигляді F = к * х ^ (1,5), де до жорсткість пружини і х є зміна в віртуальної весни довжина.

Ми моделюємо п’ять сценаріїв колиски Ньютона (як показано в наступних відео): (1) один м’яч потрапив з правого боку; (2) дві кулі вдарив з правого боку; (3) три м’ячі вдарив з правого боку; (4) чотири м’ячі вдарив з правого боку; і (5) один м’яч потрапив з обох сторін. Початкові кути удару куль встановлюються в 45 градусів. Розсіювання енергії розглядаються тут, в яких енергетичний коефіцієнт restuition встановлений на 0,96. Рухи куля починає гойдатися разом (протягом перших чотирьох випадках) або зупиняється (для п’ятого випадку) на 76.7s, 58.8s, 51.7s, 98.8s і 174.5s, відповідно.

Експеримент по маятнику Ньютона

Для того, щоб експериментально перевірити наш алгоритм, Колиска Ньютона з довжиною рядка л = 0.129m був поміщений на горизонтальному столі. П’ять однакових кульок колиски мають радіус г = 0.011m. Коефіцієнт відновлення між будь-якими двома кулями е = 0,95, а жорсткість між ними є тим же самим. Крайній лівий м’яч був піднятий і провів статичну з кутом 5π / 36 коливань, як показано на малюнку справа внизу. Початок у випуску, відео було захоплено і Хаф Circle Transform алгоритм був застосований для відстеження контури п’яти куль під час їх руху.

У таблиці в середині нижче порівнює горизонтальної швидкості п’ять куль відразу ж після того, як вони були від’єднується від першого зіткнення в експерименті та при моделюванні. Цікаво, що куля 1 рухається трохи вліво, і м’яч 4 рухається вправо зі швидкістю помітного як в експерименті та моделюванні. Це явище не може бути пояснено більш простої моделі, заснованої на збереження імпульсу і енергії тільки.

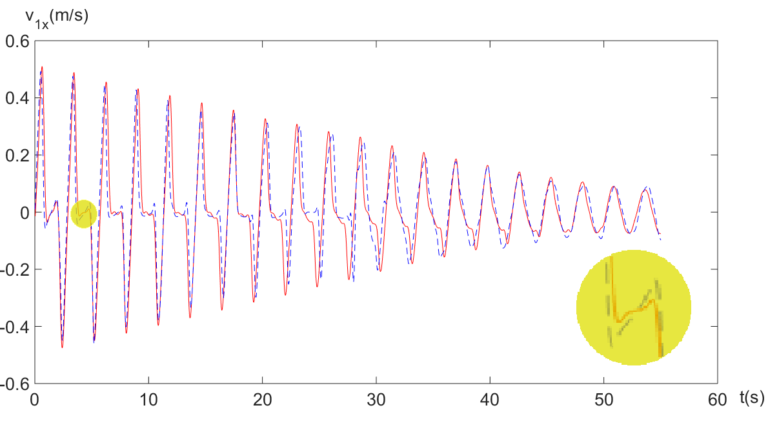
Експериментальні та результати моделювання порівнюються також уздовж осі часу, поки не більше впливу не відбулося, і всі кулі хитнувся разом. На малюнку праворуч порівнює тимчасові траєкторії горизонтальних швидкостей кулі 1, які спостерігаються в експерименті і передбачаються моделювання. Дві траєкторії збігаються дуже добре, за винятком того, що протягом кожного циклу (як показано на врізки) швидкість м’яча коливається в моделюванні трохи більше, ніж в експерименті. Це відбувається головним чином через якийсь приклеювання між кульками в експерименті, що не змодельованих.