Original: http://www.math.utah.edu/~alfeld/Archimedes/Archimedes.html
Архімед (приблизно 285 — 212 рр. до н. е.) був найвідомішим давньогрецьким математиком і 
винахідником. Він винайшов гвинт Архімеда, пристрій для підйому води, і відігравав важливу роль в обороні Сіракуз проти римської блокади, винаходячи багато військових машин, які були настільки ефективні, що вони довго затримується остаточне звільнення міста.
Коротке і в той же час змістовне обговорення Архімеда можна знайти у статті “Архімед“ в частині “Макропедія” енциклопедії Британіка.
Ось деякі посилання на інші пов’язані з Архімедом веб-сторінки:
- Ератосфен з Кірени був сучасником Архімеда (Ератосфен був приблизно на десять років молодший), і обидва відповідали з різних питань.
- Список Пі до 10 000 цифр, далеко за межі того, що цей аплет може зробити. (Він показує лише 8 цифр.)
- Біографія Архімеда.
- Земні містерії – примітки стосовно Пі.
- Джерела до теми про гвинт Архімеда.
Архімеда математична робота проявляє велику сміливість і оригінальність в думки, а також крайню суворість. Серед його математичних досягнень є обчислення пі, що відношення довжини кола до його діаметра. Його підхід полягав з вписування і обмежує правильних багатокутників з числом сторін і навколишнього середовища, і обчислення периметра цих полігонів. Це дало йому верхню і нижню межу для пі.
Якщо хто знає, що площа кола дорівнює пі раз квадрат радіусу кола, то можна також обчислити пі з цих відносин. (Звичайно, треба довести еквівалентність цих двох визначень пі.) Такий підхід до обчислень, що не використовувався до кінця 17-го століття, коли більш потужні серії розкладання на основі обчислення стали доступні.
Аплет на цій сторінці дозволяє вивчати конструкцію Архімеда в графічному вигляді і в інтерактивному режимі.
При натисканні на неї два вікна повинен з’явитися на екрані. Дві цифри поруч показують, на що вони схожі.
Вікно малюнка показує коло в червоному, вписаний багатокутник в зелений колір, і вписаного багатокутника в жовтий колір. На малюнку, вписаний багатокутник – п’ятикутник, і вписаний багатокутник – восьмикутник.
Полігони перемалювати кожен раз, коли ви вказуєте нове кількість сторін, якщо не більше, ніж пікселі боку на периферії кола. Однак наближення Пі, які відображаються на панелі управління обчислюються для будь-якої кількості сторін.
Ви можете вільно змінювати розмір вікна креслення.
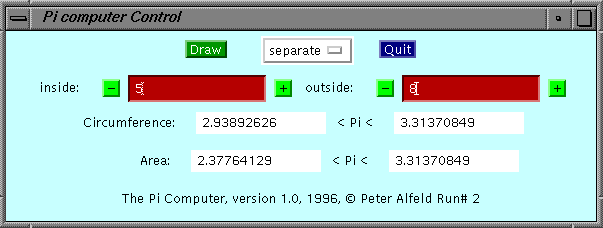
Давайте тепер обговоримо п’ять рядків вікна управління:
- Рядок 1:
- Зелена кнопка Draw відображає та приховує вікно креслення.
- Меню separate/link змушує число сторін вписаних і багатокутників рівним (посилання) або незалежний (окремий) один від одного. За замовчуванням кількість сторін вибираються незалежно один від одного.
- Блакитна кнопка Quit закриває вікно керування та вікно креслення.
- Рядок 2 містить два темно-червоний текстові поля, в якому можна вказати число сторін вписаних і багатокутників. Натискання кнопки – або + з боків текстових полів викликає відповідне число, щоб зменшити або збільшити на 1, відповідно. Найменша можлива кількість сторін, звичайно, 3, що відповідає трикутнику.
- Білі мітки в рядку 3 містять кордону пі на основі окружності.
- Рядок 4 аналогічним чином показані кордону, засновані на формулі площі. Верхня межа збігається з нижньої межі, але нижня межа гірше, ніж окружність на основі нижньої межі.
Робота у Standalone та завантаження
Ви можете завантажити байт-код даного програмного забезпечення та включити його у свої власні веб-сторінки або запустити його у вашій системі в автономному режимі. Вам потрібні такі класи Java:
При натисканні на ці посилання (які вказують на бінарні файли) ви, ймовірно, побачити щось дивне у вашій системі. Тим не менш, ви повинні мати можливість завантажувати файли належним чином, не дивлячись на їх зовнішній вигляд.
Пі є клас, який викликає всі інші. Для запуску програми в автономному режимі на системі Unix просто наберіть Java Pi в каталог, який містить файли класів. Якщо ви хочете заснувати аплету на ваших файлів не забудьте вказати код бази (каталогу, що містить файли класів) аналогічно тому, як в HTML-код цієї сторінки. Базовий код повинен бути доступний по мережі, в іншому випадку ви отримаєте виняток безпеки і речі не працюють правильно.
Якщо ви завантажити програмне забезпечення, я прошу вас, дайте мені знати, так що я можу поставити вас в моєму списку розсилки і повідомити вам про подальші удосконалень. Звичайно, також дайте мені знати, якщо у вас є якісь неприємності.
Там немає ніякої інформації, допомога вбудована в програму (по крайней мере, поки). Ця сторінка призначена, щоб бути в документації за програмою. Таким чином, ви можете скопіювати сторінку, роздрукувати або вказати посилання на нього.
[1 квітня 1999 р.]
Назад до головної сторінки Пітера Альфельда.
Розроблено для netscape і Java.
