Original: http://www.stat.yale.edu/Courses/1997-98/101/binom.htm
У багатьох випадках доцільно узагальнити групу незалежних спостережень числа спостережень в групі, які представляють собою один з двох результатів. Наприклад, частка осіб у випадковій вибірці, які підтримують одну з двох політичних кандидатів відповідає цьому опису. В цьому випадку статистичне 
є підрахунком X виборців, що підтримують кандидата, поділене на загальне число особин в групі n. Це дає оцінку параметра p, частки осіб, які підтримують кандидата в сукупності.
Біноміальний розподіл описує поведінку змінного лічильника X, якщо виконуються наступні умови:
1: Число спостережень n фіксоване.
2: Кожне спостереження є незалежним.
3: Кожне спостереження являє собою один з двох результатів (“успіху” або “невдачі“).
4: Імовірність “успіху” p є однаковим для кожного результату.
Якщо ці умови виконані, то Х має біноміальний розподіл з параметрами n і p, скорочено B(n,p).
Приклад
Нехай люди з певним геном має 0,70 ймовірність зараження в кінцевому рахунку певного захворювання. Якщо 100 особин з геном брати участь в житті дослідженні, то розподіл випадкової величини, яке описує кількість осіб, які будуть контрактом захворювання розподіляється B(100,0,7).
Примітка. Розподіл вибірки змінного лічильника тільки добре описується біноміальним розподілом є випадками, коли розмір популяції значно більше, ніж розмір зразка. За загальним правилом, біноміальний розподіл не повинно бути застосоване до спостережень з простої випадкової вибірки (SRS), якщо розмір популяції не є, щонайменше в 10 разів більше, ніж розмір зразка.
Для того, щоб знайти ймовірності від біноміального розподілу, можна або обчислити їх безпосередньо, використовувати біноміальними таблицю, або використовувати комп’ютер. Кількість шісток прокату на одному кристалі в 20 валків має B(20,1/6) розподілу. Імовірність прокатки більше 2 шістки в 20 рулонів, P(X>2), дорівнює 1 – P(X<2) = 1 – (P(X=0) + P(X=1) + P(X=2)). Використовуючи Minitab команди “cdf” з підкоманду “binomial n=20 p=0.166667” дає інтегральну функцію розподілу наступним чином:
Binomial with n = 20 and p = 0.166667 x P( X <= x) 0 0.0261 1 0.1304 2 0.3287 3 0.5665 4 0.7687 5 0.8982 6 0.9629 7 0.9887 8 0.9972 9 0.9994
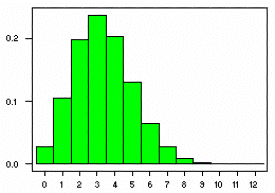
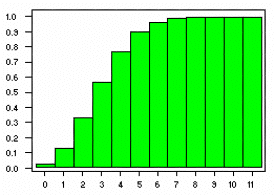
Відповідні графіки для функції щільності ймовірності та функції розподілу для B(20,1/6) розподілів наведені нижче:
Оскільки ймовірність 2 або менше шістки дорівнює 0,3287, ймовірність прокатки більше 2 шістки = 1 – 0,3287 = 0,6713.
Імовірність того, що випадкова величина Х з біноміальним розподілом B(n,p) дорівнює значенню k, де k = 0, 1,….,n , задається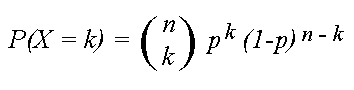 
де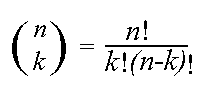 
Останній вираз відомо як біноміальний коефіцієнт, заявив, як “n choose k” або число можливих способів вибору k “успіхам” з n спостережень. Наприклад, число способів досягти 2 головки в наборі з чотирьох кидків є “4 choose 2” або 4!/2!2! = (4*3)/(2*1) = 6. Можливості {HHTT, HTHT, HTTH, TTHH, THHT, THTH}, де “H” позначає головку і “Т” є хвіст. Біноміальний коефіцієнт примножує ймовірність одну з цих можливостей (який є (1/2)²(1/2)² = 1/16 для справедливої монети) по числу способів результат може бути досягнутий, для повної ймовірності від 6/16.
Середнє значення і дисперсія біноміального розподілу
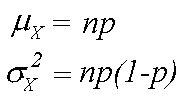
Приклади пропорцій
Якщо ми знаємо, що кількість X “успіхів” у групі з n спостережень з ймовірністю успіху і р має біноміальний розподіл з середнім нп і дисперсією np(1-p), то ми можемо отримати інформацію про розподіл вибірки питома вага, кількість успіхів X ділиться на число спостережень n. За мультиплікативні властивості середнього значення, середнє значення розподілу X/n дорівнює середньому значенню X, поділеній на n, або np/n = p. Це доводить, що зразок пропорція є несмещенной оцінкою населення частки p. Дисперсія X/n дорівнює дисперсії X, поділеній на n², або (np(1-p))/n² = (p(1-p))/n. Ця формула показує, що, як розмір зразка збільшується, дисперсія зменшується.
У прикладі прокатки шестистороннього вмирають в 20 разів, то ймовірність р прокатки шість на будь-якому рулоні дорівнює 1/6, і кількість X має шістки розподілу B(20, 1/6). Середнє це розподіл 20/6 = 3,33, а дисперсія становить 20 * 1/6 * 5/6 = 100/36 = 2,78. Середнє значення частки шістки в 20 рулонів, X/20, так само р = 1/6 = 0,167, а дисперсія частки дорівнює (1/6 * 5/6)/20 = 0,007.
Нормальне наближення для графів і пропорцій
Для великих значень n, розподілу лічильника X і зразок пропорції приблизно нормальні. Цей результат випливає з центральної граничної теореми. Середнє значення і дисперсія для приблизно нормального розподілу X є np і np(1-p), ідентичний середнього і дисперсії біноміального розподілу (n,p). Аналогічним чином, середнє значення і дисперсія для приблизно нормального розподілу зразка пропорції є р і (p(1-p)/n).
Примітка. Оскільки нормальне наближення не є точним для малих значень п, гарне правило полягає в тому, щоб використовувати нормальне наближення, тільки якщо np>10 and np(1-p)>10.
Наприклад, розглянемо популяцію виборців в даному стані. Справжня частка виборців, які виступають за кандидата А, дорівнює 0,40. З огляду на зразок 200 виборців, наскільки ймовірним є те, що більше половини виборців підтримати кандидата А?
Кількість Х виборців в зразку 200, які підтримують кандидата А розподіляється B(200,0,4). Середнє значення розподілу дорівнює 200 * 0,4 = 80, а дисперсія дорівнює 200 * 0,4 * 0,6 = 48. Стандартне відхилення являє собою квадратний корінь з дисперсії, 6,93. Імовірність того, що більше половини виборців в зразку кандидата підтримка А дорівнює ймовірності того, що Х більше 100, яка дорівнює 1- P(X< 100).
Для того, щоб використовувати нормальне наближення для розрахунку цієї ймовірності, ми повинні спочатку визнати, що нормальний розподіл є безперервним і застосувати корекцію безперервності. Це означає, що ймовірність для одного дискретного значення, наприклад, 100, поширюються на ймовірність інтервалу (99,5, 100,5). Оскільки ми зацікавлені в тому, ймовірність того, що X менше або дорівнює 100, нормальне наближення відноситься до верхньої межі інтервалу, 100,5. Якби ми були зацікавлені в ймовірності того, що X строго менше 100, то ми б застосувати нормальне наближення до нижнього кінця інтервалу, 99,5.
Таким чином, застосовуючи корекцію безперервності і стандартизація змінної X дає наступне:
1 – P(X< 100)
= 1 – P(X< 100,5)
= 1 – P(Z< (100,5 – 80)/6,93)
= 1 – P(Z< 20,5/6,93)
= 1 – P(Z< 2,96) = 1 – (0,9985) = 0,0015. Так як значення 100 є майже три стандартним відхиленням від середнього 80, ймовірність спостереження підрахунку цього високого вкрай мала.
