Original: http://www.math.stonybrook.edu/~tony/mazes/satmaze.html
Тоні Філіпс/Tony Phillips
Через лабіринти до математики
Найвідоміший з цих лабіринтів – критський лабіринт. Це можна намалювати як гру.
Ось ще один приклад. Цей лабіринт фігурує в декількох середньовічних івритських рукописах. Хоча цей лабіринт має поверхневу схожість на критський лабіринт, близьке порівняння показує, що вони зовсім інші. Єрихонський лабіринт має 7 рівнів, тоді як Критський лабіринт має 8, і послідовність, в якій досягаються рівні, відрізняється від одного лабіринту до іншого. В обох лабіринтах шлях прямує до рівня 3 (рахуючи зовнішній вигляд як 0), але в Критському лабіринті він подвоюється назад через рівні 2 та 1, тоді як в лабіринті Єрихону він продовжується через рівні 4 та 5 до повернення до рівня 2 та 1 1. Повні послідовності рівня є
Критський 032147658
Єрихон 03452167.
Властивості, якими поділяються ці два лабіринти, і які слугуватимуть для визначення класу лабіринтів з простим математичним описом, можна узагальнити, називаючи їх простими, чергуючими, транзитними лабіринтами (лабіринтами).
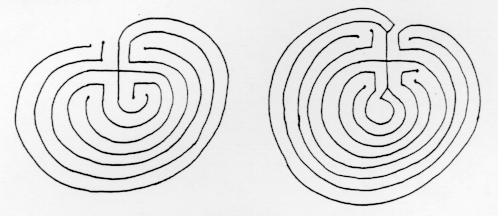ТРАНЗИТНИЙ лабіринт, тому що шлях проходить без роздвоєння ззовні лабіринту до центру. Наприклад, ці лабіринти не є транзитними лабіринтами: в одному, шлях виходить на тій же стороні, в яку він увійшов; а в іншому є точки, де лабіринт повинен вибрати, яким шляхом рухатися.
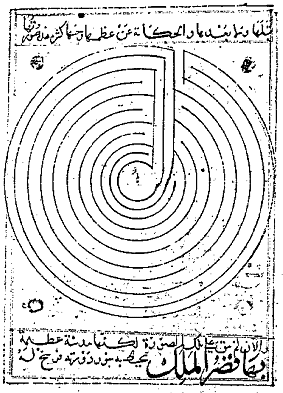ЗМІННИЙ, оскільки план лабіринту викладений на певній кількості концентричного або паралельного рівнів, а шлях лабіринту змінює напрямок кожного разу, коли він змінюється рівнем. Наприклад, цей лабіринт, який відображає план Константинополя в середньовічній книзі з географії арабської географії, має чіткі рівні, але не чергується, оскільки він спирається від рівня 10 до рівня 1 без зміни напрямку. Її послідовність рівнів 0.3.4.5.6.7.8.9.10.1.2.11, як ми побачимо, не може відбуватися як послідовність рівнів змінного лабіринту.
ПРОСТИЙ, тому що шлях складає по суті повне коло на кожному рівні; зокрема він подорожує на кожному рівні рівно один раз. Наприклад, цей чергується транзитний лабіринт, який зустрічається як лабіринт тротуару в Шартрі (показаний тут) та в декількох інших соборах, і вирізаний на стовпі в соборі в Лукці, не простий: є чотири різних точки, на які йде шлях може змінювати рівні. Цей лабіринт, здається, стався як християнська розробка та розширення критського дизайну та його римських нащадків; асоціація з міфом Тесея зберігалася. Новий дизайн був надзвичайно стійким. Він помітний у середньовічних рукописах, що датуються 9 століттям; Собор Шартр був побудований близько 1200 року; а на початку 16 століття ідентичний візерунок намальований на флорентійському кассоні. Зараз він зроблений 3-х розмірним, броньований Тесей бореться з Мінотавром у центрі.
ТОПОЛОГІЯ простих, змінних і транзитних лабіринтів повністю визначається їх послідовностями рівнів.
Тоні Філіпс
17 березня 2015 р.
