Original: http://robotics.cs.iastate.edu/ResearchSimultaneousImpacts.shtml

Цей проект був початий в протягом 6-місячного суботнього візиту Ян-Bin з Метью Т. Мейсон і Майкл Ердмана в університеті Карнегі-Меллона в 2007 році, і з тих пір продовжував в першу чергу в Університеті штату Айова і в Китаї (в перервах). Згідно нашої моделі, зіткнення з декількома тіла в імпульсному просторі, як діаграма переходів стану, в якому кожне стан являє собою фазу, протягом якого дія “активні” при тільки підмножина точок контакту. В ході зіткнення, вплив може стати активні і неактивні кілька разів, в залежності від того, обидві що тіла миттєво проникають одна в одну чи ні. Стан переходу відбувається всякий раз, коли активний вплив закінчує реституцію або неактивний вплив отримує відновлено. Пружна енергія через вплив не тільки залежить від імпульсу у відповідній точці контакту, але і іншими імпульсами, що впливають на двох залучених органів в тривалості цього впливу. імпульсу на основі закону Пуассона реституції може привести до негативної енергії. Наш новий закон про реституцію регулює втрату пружної енергії під час фази. Результат зіткнення залежить від співвідношення контактних жорсткостей, а не на їх індивідуальних значень.

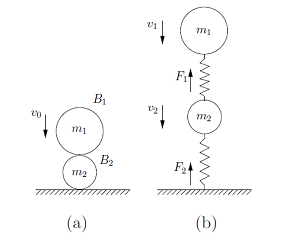
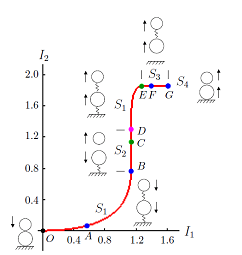
У представницькому випадку кулі, що падає на інший на столі (показано зліва нижче), два удари, один між двома кулями, а інший між нижнім шаром і столом. Крива, що описує зростання двох імпульсів нанесені червоним кольором на малюнку справа для примірника зіткнення. Початкова конфігурація звертається поруч з походження з центрами двох кульок вертикально. Процес зіткнень описується в термінах накопиченнями I1 і I2 імпульсів на балу-м’яч і м’яч-таблиці контактів, відповідно. Він розпадається на послідовність з п’яти станів S1, S2, S1, S3, S4, які відповідають п’яти сегментів наростів (I1, I2): [О, В), [B, D), [D, E) , [Е, G), і G. на малюнку кожне стан збільшується з конфігурацією, під час стану, в якому активні контакти представлені в вигляді (віртуальних) джерел.

Одночасні колізій між декількома органами

Модель багаторазового впливу може бути інтегрована з декількома копіями моделі complient удару, щоб вирішити загальну проблему одночасного багатотільних зіткнень. Це робиться за допомогою розкладання:

*Модель багаторазового впливу визначає набір миттєво активних контактів і формує нормальні імпульси на цих контактах на основі їх диференціальних відносин.
*При кожному контакті, модель відповідає вплив отримати тангенціальний імпульс від нормального імпульсу за допомогою аналізу в контактному режимі енергії на основі.
*Нормальні і дотичні імпульси потім об’єднуються в якості внеску в динаміку системи для поновлення швидкостей тіл при зіткненні.

Моделювання більярдні Shots

Модель зіткнення застосовується до більярдного зйомки, в якому удари кия биток, який, в свою чергу, впливає більярдний стіл. Більярдний з деякою початковою швидкістю і кутової швидкості, як правило ковзає по параболічної дузі на більярдному столі і прокатки, перш ніж він почне по прямій траєкторії. На початковому етапі цього дослідження, ми вивчаємо рух битка, повідомляється кия. Цей рух є результатом одночасних зіткнень між києм і кулею, і м’яч і більярдний стіл. До сезам зараз, наші зусилля зосереджені на розробці моделі впливу для одночасних фрикційних впливів. Тема була предметом суперечок для того, щоб бути у відповідності з законом Кулона тертя, гіпотези Пуассона про реституцію, і закон збереження енергії.

Крайня ліва цифра нижче ілюструє два одночасних впливів: один між кінчиком кия і битка, а інший між битком і столом. На другому малюнку нижче ділянки позиції (точки) кулі в центрі кожні 1/30-ї секунди під час його руху, захоплене камерою, слідуючи за постріл масово. Також показані траєкторії підходять по цих позиціях поряд з параболи, а лінія, на якій був переміщений м’яч. (Зверніть увагу, що крайня ліва точка являє собою лише останню позицію, перш ніж м’яч покинув поле камери зору.) Третій малюнок нижче на лівому фланзі і показує відновлену траєкторію за інтегральною моделлю впливу – він схожий на фактичної траєкторії. Прогнозовані швидкості після пострілу битка лише незначно відрізняються від обчислених з відео-захоплена траєкторії.

Наша довгострокова мета полягає в тому, щоб створити робота, здатного грати в більярд з навичками людського рівня на основі розуміння механіки. Ми будемо інтегрувати роботу з інших областей, включаючи бачення, контролю, механіки та планування. Існуючі системи більярдна робота зосередитися або на бачення завдання розпізнавання і локалізації куль і позиціонування кий, або на виконанні простих пострілів під керівництвом алгоритму навчання, нечіткої експертної системи, або сірої теорії прийняття рішень. Наскільки нам відомо, жоден з розроблених систем не виробляють постріли, засновані на механіці більярду, або виставлені попередні навички стрільби.

Ян-бен Цзя, Метью Т. Мейсон, і Майкл А. Ердман. Діаграма перехідного стану для одночасних зіткнень із застосуванням в більярдному стрільби. Представлений на міжнародному семінарі з Восьмий алгоритмічних Основи робототехніки, Гуанахуато, Мексика, грудень 2008 року.
Ян-бен Цзя, Метью Т. Мейсон, і Майкл А. Ердман. Багаторазові ударні навантаження: перехідний стан схема заходу на посадку. (672K, 63 сторінки). Міжнародний журнал Robotics досліджень, Vol. 32, немає. 1, стор. 84-114, 2013 роки