Original: http://it.stlawu.edu/%7Edmelvill/mesomath/sumerian.html
Приблизно 3000 р. до н.е. шумери малювали образи токенів на глиняних табличках. На даний момент різні види товарів були представлені різними символами, а також множинні кількості представлені повторенням. Три одиниці зерна були позначені три “хлібних знаки”, п’ять банок оліїа позначалися як п’ять “олійних марок” і так далі.
Є два важливих обмеження такої системи. По-перше, будь-який інший тип товару, для якого ви хочете зробити запис повинна мати свій власний відмітний знак. Ми бачили, як зростаюча складність економічного життя призвело до значного поширення стилів маркерів. Кожен з цих маркерів в даний час мало бути винесено за своїми власними знаком, і, звичайно ж, все знаки повинні були бути вивчені. Друге обмеження стосується не асортименту товарів, доступних, але їх кількість. Запис доставки або виділення трьох банок олії, написавши символу глечик олії три рази просто і зручно. Запису не доставку або витрачання кількох сотень банок масла точно так же вже не так зручно, а також є система схильна до помилок. Великі храмові комплекси, які розвивалися в кінці четвертого тисячоліття, такі як храм Інанни в Уруці, були значні економічні підприємства, що займаються в великих кількостях товарів і праці. Поступово, нова система повинна була бути розроблена.
Перше велике нововведення після акту написання був поділ кількості хорошого від символу на благо. Тобто, щоб представити три одиниці зерна символом “три”, за яким слідує символ “хлібної одиниці” таким же чином, що ми будемо писати 3 вівці або 3 корови або, у більш загальному плані, 3 літри або 3 кілометри. Система такого роду є метрологічна система числення, система заходів і терезів. Символ “три” не є повністю абстрактним, але дається значення його контекстом, маючи одиниці прикладених. Розвиток цієї концепції протягом третього тисячоліття є захоплюючим і надзвичайно складна історія, яка ще тільки частково зрозумів.
У той час як ми використовуємо одні й ті ж знаки з цифрами, незалежно від їх метрологічного сенсу (“3” для овець є той же знак, як “3” для кілометрів або банки олії), шумери використовували широкий спектр різних символів. Ніссен, Дамер і Енглунд виявили близько 60 різних знаків числа, які вони групи в дюжині або так метрологічних систем (див. розділ 6 “Архаїчної бухгалтерії”). Наприклад, шумери використовували одну систему для підрахунку дискретних об’єктів, таких як тварини, й інші системи для вимірювання площ або обсягів. Кожна система мала набір знаків, що позначають різні кількості.
Будь-яка метрологічна система містить ряд різних розмірів блоків із фіксованими коефіцієнтами перерахунку між ними, так що, наприклад, є 12 дюймів в нозі і три фути у дворі, і так далі. Так само, як в наших старих вагових систем і вимірювання, шумерська метрологія були представлені всі види коефіцієнтів перерахунку, хоча слід зазначити, що всі вони були прості дроби 60.
У базовій шістдесятковій системі використовується для підрахунку більшості дискретних об’єктів, один об’єкт, вівця або корова або риба, позначається невеликим конусом. Десять конусів склав один невелике коло, шість маленьких гуртків дорівнював один великий конус, десять великих конусів дорівнював був великий конус з колом усередині нього, шість з них був великий круг і десять великих кіл було дано велике коло з невеликим колом всередині. Цей останній блок був тоді вартий 10x6x10x6x10 = 36000 базових величин. Зверніть увагу, що коло і “конус-форма” може бути легко зроблено за допомогою стилуса натисканні на глину, або вертикально по колу або під кутом для конуса.
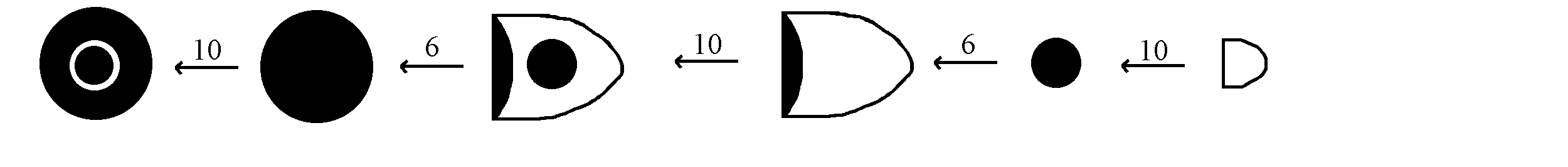
Для дискретних раціонів товарів “бішістдесятинна” система була використана з конверсією факторів 10, 6, 2, 10 і 6, так що символ для найбільшої кількості, на цей раз велике коло, що містить два маленьких кола, що позначається 6x10x2x6x10 = 7200 базових величин.
Ще одна система використовувалася для вимірювання потужності зерна. Тут коефіцієнти перерахунку були 5, 10, 3, і 10, так що найбільший блок, великий конус, що містить невелике коло, варто 10x3x10x5 = 1500 малих одиниць.
Додавання до плутанини для сучасних вчених, які намагаються розгадати ці складні метрологічні системи був той факт, що один знак може бути використаний в декількох системах, де це може означати різні кратні базового блоку. Зокрема, мале коло може означати, 6, 10 або 18 маленьких конуса, в залежності від контексту (а також інші кратні базових блоків, позначеними іншими символами). Приклад архаїчної таблиці раціону див. тут.
Поступово, протягом третього тисячоліття, ці знаки були замінені клинописних еквіваленти, так що цифри можуть бути записані з тим же стилусом, який використовувався для слів в тексті.
Останнім кроком в цій історії, ймовірно, відбувається деякий час в період Ур III, в самому кінці третього тисячоліття, стало введення системи шістдесяткова місце значення. Кількість знаків було скорочено до двох: вертикальний клин, похідний від малого конуса часто використовується для базового блоку і кутового клина, отриманий з малого кола. Кут клина мала значення десяти вертикальних клинів. В системі підрахунку шістдесяткова, описаної вище, наступний блок розміром був великий конус, коштує шість кіл. В системі місце значення, даний пристрій було позначено одним і тим же розміром вертикального клина в якості базового блоку, і це коштувало шість кутових клинів. Тепер пара символів може бути повторена в нескінченно більшому знакозмінного ряду кутових і вертикальних клинів, завжди зберігаючи ті ж коефіцієнти перетворення 10 і 6. Розплата була що вертикальний клин тепер може означати 1 або 60 (6×10) або 3600 (60×60), і так далі. Його фактичне значення було визначено його місце.
Система шістдесяткова місце значення значно полегшило розрахунки, але, звичайно ж, врешті-решт, остаточну відповідь повинен був бути переведений назад в основний метрологічної системи одиниць. Таким чином, проблема буде вказано у відповідних одиницях і рішення буде дано у відповідних одиницях, але проміжні розрахунки проводилися в новій системі шістдесяткова місце значення.
Подальше читання: Безсумнівно, найкраще обговорення цієї теми тут: Архаїчна бухгалтерія.
Востаннє змінено: 3 жовтня 2002 року
Дункан Дж. Мелвілл