Original: http://people.math.gatech.edu/~thomas/FC/fourcolor.html
Ця сторінка подає стислу інформацію про новий доказ теореми чотирьох кольорів і алгоритму чотирьох фарб від Ніла Робертсона, Даніеля П. Сандерса, Пола Сеймура і Робіна Томаса.
Зміст:
- Історія.
- Чому новий доказ?
- Схема доказу.
- Основні аспекти нашого доказу.
- Конфігурації.
- Правила виписування.
- Вказівники.
- Квадратичний алгоритм.
- Обговорення.
- Посилання.
Історія.
Проблема чотирьох кольорів походить від 1852 р., коли Френсіс Гатрі, намагаючись пофарбувати карту графств Англії зауважив, що чотирьох кольорів вистачило. Він попросив свого брата Фредеріка, якщо це правда, що будь-яка карта може бути пофарбований, використовуючи чотири кольори таким чином, щоб сусідні ділянки (тобто тих, хто розділяє загальний сегмент граничної, а не тільки точку) отримувати різні кольори. Фредерік Гатрі потім передав гіпотезу до онального. Перша друкована посилання обумовлена Кейлі в 1878 році.
Через рік перший “доказ” Кемпа з’явився; його неправильності було зазначено на роботі Хівуда 11 років по тому. Іншим не вдалося через доказ Тету в 1880 році; пробіл в аргументі було відзначено Петерсеном в 1891. Обидва зазнали невдачі докази дійсно було якесь значення, хоча. Кемпе виявив, що стало відомо як Кемпе ланцюгами, і Тейт знайшов еквівалентну формулювання чотирьох колірних теореми в термінах 3-реберної розмальовці.
Наступним важливим внеском прийшов з Біркгофом, чия робота дозволила Франкліну в 1922 році довести, що гіпотеза чотирьох кольорів вірна для відображень з не більше ніж 25 регіонах. Вона також використовується іншими математиками, щоб зробити різні форми прогресу з проблеми чотирьох фарб. Слід зазначити, зокрема, Хееш, який розробив дві основні компоненти, необхідні для остаточного доказу – редуціруеми і вивантаження. Хоча концепція зводиться була вивчена іншими дослідниками, а також, мабуть, що ідея розрядки, має вирішальне значення для невідворотності частини докази, через Хееш, і що саме він висловив припущення, що відповідний розвиток цього методу буде вирішити чотири кольори проблеми.
Це було підтверджено Аппеля і Хакена в 1976 році, коли вони опублікували своє підтвердження теореми чотирьох кольорів [1,2].
Чому новий доказ?
Є дві причини, чому доказ Аппеля-Хакена не є повністю задовільним.
• Частина докази Аппеля-Хакена використовує комп’ютер, і не можуть бути перевірені вручну, і
• навіть та частина, яка нібито рука перевіряється є надзвичайно складним і виснажливим, і, наскільки нам відомо, ніхто не перевірив його в повному обсязі.
Фактично ми намагалися перевірити доказ Аппеля-Хакена, але незабаром здався. Перевірка комп’ютера частина не тільки вимагає багато програмування, але і введення опису 1476 графів, і це було навіть не сама спірна частина докази.
Ми вирішили, що було б вигідніше працювати наше власне доказ. Таким чином, ми зробили і придумали докази і алгоритм, які описані нижче.
Схема доказу.
Основна ідея докази така ж, як у Аппеля і Хакена. Ми виставляємо набір 633 “конфігурацій”, і довести, кожен з них є “приводиться”. Це технічна концепція, яка передбачає, що ніяка конфігурація з цією властивістю не може з’явитися в мінімальний контрприклад до теоремі чотирьох кольорів. Він також може бути використаний в алгоритмі, для якщо приводиться конфігурації з’являється в плоскому графі G, то можна побудувати в постійній часу менший планарний граф G’, що будь-які чотири-розмальовка G’ може бути перетворений в чотирьох- розфарбування G в лінійному часу.
Це було відомо з 1913 року, що кожен мінімальний контрприклад до чотири кольори теорема є внутрішньо 6-підключений тріангуляції. У другій частині докази ми доведемо, що принаймні один з наших 633 конфігурацій з’являється в кожному всередині 6-пов’язаної плоскою тріангуляції (не обов’язково мінімальний контрприклад до 4CT). Це називається доводить невідворотність, і використовує “Розрядка метод”, вперше запропонований Хеешем. При цьому наш метод відрізняється від Аппеля і Хакена.
Основні аспекти нашого доказу.
Ми підтверджуємо гіпотезу Хееша, що при доведенні невідворотність, що приводиться конфігурації можна знайти в другій міста “переплачує” вершини; це те, як ми уникаємо “занурення” проблеми, які були основним джерелом ускладнення для Аппель і Хакен. Наш неминучий набір розмір 633, на відміну від безлічі 1476 членів Аппеля і Хакена, і наш метод розрядка використовує тільки 32 правила вивантаження, замість 300 + Аппеля і Хакена. Нарешті, ми отримуємо квадратний алгоритм на чотири кольори плоских графів (описаних нижче), поліпшення в порівнянні з квартіке алгоритму Аппеля і Хакена.
Конфігурації.
Близьке-тріангуляції є ненульовим підключений без петель плоский граф таким чином, що кожна кінцева область являє собою трикутник. Конфігурація K складається з майже тріангуляції G і відображення g з V (G) до цілих чисел з наступними властивостями:
- Для кожної вершини v, G\v має принаймні два компоненти, і якщо їх два, то рівень v складає g(v)-2,
- Для кожної вершини v, якщо v не є інцидентом із нескінченної області, g(v) відповідає рівню v, а інакше g(v) перевищує рівень v; і в будь-якому випадку g(v)> 4,
- K має кільцевий розмір щонайменше 2, де кільцевий розмір K визначено як суму g(v)-deg(v)-1, зібрану з усіх вершин v інцидента з нескінченної області, наприклад, G\v пов’язано.
При кресленні зображень конфігурацій ми використовуємо конвенції, введені Хеешем. Форми вершин вказують значення g(v) у такий спосіб: твердий чорний коло означає g(v) = 5, точка (або те, що з’являється на зображенні, як не символ взагалі) означає, що g(v) = 6, порожнистий коло означає g(v) = 7, порожнистий квадрат означає g(v) = 8, трикутник означає g(v) = 9, а п’ятикутник означає g(v) = 10. (Нам не потрібні вершини v з g(v) > 11, і тільки одна вершина з g(v) = 11, для яких ми не використовуємо жодних спеціальних символів.) Зображене на малюнку 17 наших 633 приводяться конфігурацій відображаються за допомогою зазначеної конвенції. Весь набір можна переглянути, натиснувши тут. (Ми маємо на увазі (3.2) нашій роботі <a href="http://people.math.gatech.edu/~thomas/FC/fourcolor commander viagra.html#References”>[7] для значення “товстих країв” і “полуребер” в цих картинах.)
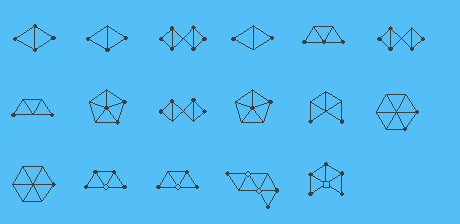
Будь-яка конфігурація ізоморфна одній із 633 конфігурацій, виставлені в [7] називається хорошою конфігурацією. Нехай Т тріангуляції. З’явиться конфігурація K=(G,g) в Т, якщо G є подграфа Т, кожна кінцева область G являє собою область Т, а g(v) дорівнює ступеня v в Т для кожної вершини v з G. Доведемо такі два твердження.
ТЕОРЕМА 1. Якщо T є мінімальний контрприклад до теоремі чотири кольори, то ніяка гарна конфігурація не з’являється в T.
ТЕОРЕМА 2. Для кожного всередині 6-підключеного тріангуляції Т, деяка хороша конфігурація з’являється в T.
З наведених вище двох теорем випливає, що жоден мінімальний контрприклад не існує, і тому 4СТ вірно. Перший доказ потрібен комп’ютер. Другий може бути перевірений вручну протягом декількох місяців, або, за допомогою комп’ютера, він може бути перевірена протягом приблизно 20 хвилин.
Правила виписування.
Нехай Т внутрішньо 6 з’єднаних тріангуляції. Спочатку кожна вершина v присвоюється заряд 10(6-deg(v)). З формули Ейлера, що сума зарядів всіх вершин 120; зокрема, вона позитивна. Тепер ми перерозподілити витрати відповідно до таких правил, в такий спосіб. Щоразу, коли Т має подграфа, изоморфного одному з графіків на малюнку нижче, які відповідають специфікації ступеня (для вершини v з правила з негативним знаком поруч з v це означає, що ступінь відповідної вершини Т не перевищує значення визначається формою v, і аналогічно для вершин зі знаком плюс поруч з ними, потрібно рівність для вершин без знака поруч з ними) заряду одного (двох в разі першого правила) повинен бути спрямований уздовж край, зазначений стрілкою.
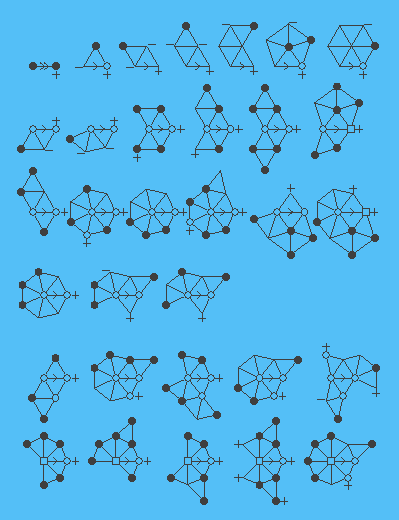
Ця процедура визначає новий набір зарядів з тієї ж загальної суми. Так як загальна сума позитивна, є вершина v в Т, новий заряд позитивний. Покажемо, що хороша конфігурація з’являється в другій околиці v.
Якщо ступінь v становить не більше 6 або щонайменше 12, то це можна побачити досить легко прямим аргументом. Для інших випадків, однак, докази набагато складніше. Тому ми написали докази на формальній мові, так що вони можуть бути перевірені за допомогою комп’ютера. Кожен етап цих доказів є людиною, що перевіряються, але самі докази насправді не перевіряється вручну, через їх довжини.
Вказівники.
Теоретична частина нашого докази описана в [7]. Огляд 10-сторінка доступна он-лайн. Комп’ютерні дані та програми, які використовуються для бути розташовані на анонімний сервер FTP, але цей сервер було припинено. Одні і ті ж файли, тепер доступні з http://www.math.gatech.edu/~thomas/OLDFTP/four/ і може бути зручно переглядати. Незалежний набір програм була написана Гаспером Фіджавцем під керівництвом Боян Могар.
Квадратичний алгоритм.
Вхід алгоритму буде плоскою тріангуляції G з п вершинами. (Це без обмеження спільності, так як будь-який плоский граф може бути тріангулірованная в лінійному часу.) Вихідний сигнал буде розфарбування вершин G з чотирма кольорами.
Якщо G має не більше чотирьох вершин кольору кожна вершина іншого кольору. В іншому випадку, якщо G має вершину х ступеня до <5, то схема C навколо нього є “k-кільце”. Перехід до аналізу k-кільця нижче. В іншому випадку G має мінімальну ступінь п’ять. Для кожної вершини ми обчислимо його заряд, як описано вище, і знайти вершину v позитивного заряду. З доведення теореми 2 випливає, що або хороша конфігурація з’являється в другій околиці v (це разі чого він може бути знайдений в лінійному часу), або до-кільце порушивши визначення внутрішнього 6-підключення можна знайти в лінійний час. В останньому випадку ми перейти до аналізу k-кільця нижче, в першому випадку ми застосовуємо рекурсию до деякого меншого графа. Чотирьох-розмальовка G, то можна побудувати з чотирьох-розмальовки цього меншого графа в лінійному часу.
З огляду на k-кільця R, що порушує визначення внутрішнього 6-з’єднання може бути використана процедура, розроблена Біркгофом. Ми застосовуємо рекурсию двох ретельно відібраних подграфов G. четирехштанговой забарвлення G, то можна побудувати з чотирьох-розмальовок двох менших графів в лінійний час.
Обговорення.
Слід зазначити, що обидві наші програми використовують тільки целочисленную арифметику, і тому ми не повинні бути пов’язані з помилками округлення і інших аналогічних небезпек арифметики з плаваючою точкою. Проте, аргумент може бути зроблено, що наш “доказ” не є доказом у традиційному сенсі цього слова, тому що він містить кроки, які ніколи не можуть бути верифіковані людьми. Зокрема, ми не довели правильність компілятора компільованою наші програми на, ні ми довели непогрішність апаратних засобів ми зіткнулися наші програми на. Вони повинні бути прийняті на віру, і, імовірно, є джерелом помилок. Однак, з практичної точки зору, ймовірність комп’ютерної помилки, яка з’являється послідовно точно таким же чином, на всіх прогонів наших програм на всіх укладачів під усіма операційними системами, що наші програми працюють на мізерно мала в порівнянні з шансом людської помилки під час того ж кількості прецедентним перевірки. Крім цієї гіпотетичної можливості комп’ютера послідовно дає неправильну відповідь, інші наші докази можуть бути перевірені таким же чином, як і традиційні математичні докази. Ми визнати, однак, що перевірка комп’ютерної програми набагато складніше, ніж перевіряти математичне доказ тієї ж довжини.
Подяки.
Ми зобов’язані Томасу Фаулеру, Крістоферу Карлу Хекману і Барретту Уоллсу за їх допомогу з підготовкою до цієї сторінки. Наша робота була частково підтримана Національним науковим фондом.
Посилання.
- K. Appel and W. Haken, Every planar map is four colorable. Part I. Discharging, Illinois J. Math. 21 (1977), 429-490.
- K. Appel, W. Haken and J. Koch, Every planar map is four colorable. Part II. Reducibility, Illinois J. Math. 21 (1977), 491–567.
- K. Appel and W. Haken, Every planar map is four colorable, Contemporary Math. 98 (1989).
- G. D. Birkhoff, The reducibility of maps, Amer. J. Math. 35 (1913), 114-128.
- H. Heesch, Untersuchungen zum Vierfarbenproblem, Hochschulskriptum 810/a/b, Bibliographisches Institut, Mannheim 1969.
- A. B. Kempe, On the geographical problem of the four colors, Amer. J. Math., 2 (1879), 193-200.
- N. Robertson, D. P. Sanders, P. D. Seymour and R. Thomas, The four colour theorem, J. Combin. Theory Ser. B. 70 (1997), 2-44.
- N. Robertson, D. P. Sanders, P. D. Seymour and R. Thomas, A new proof of the four colour theorem, Electron. Res. Announc. Amer. Math. Soc. 2 (1996), 17-25 (електронна версія).
- T.L. Saaty, Thirteen colorful variations on Guthrie’s four-color conjecture, Amer. Math. Monthly 79 (1972), 2-43.
- T.L. Saaty and P. C. Kainen, The four-color problem. Assaults and conquest, Dover Publications, New York 1986.
- P. G. Tait, Note on a theorem in geometry of position, Trans. Roy. Soc. Edinburgh 29 (1880), 657-660.
- H. Whitney and W. T. Tutte, Kempe chains and the four colour problem”, in Studies in Graph Theory, Part II (ed. D. R. Fulkerson), Math. Assoc. of America, 1975, 378-413.
13 листопада 1995 року
